Heat soak is the last thing you want in a speed density system.

The entire premise of engine load calculation is derived from the displacement of the engine, the manifold pressure, an efficiency table that is calibrated, and air temperature.

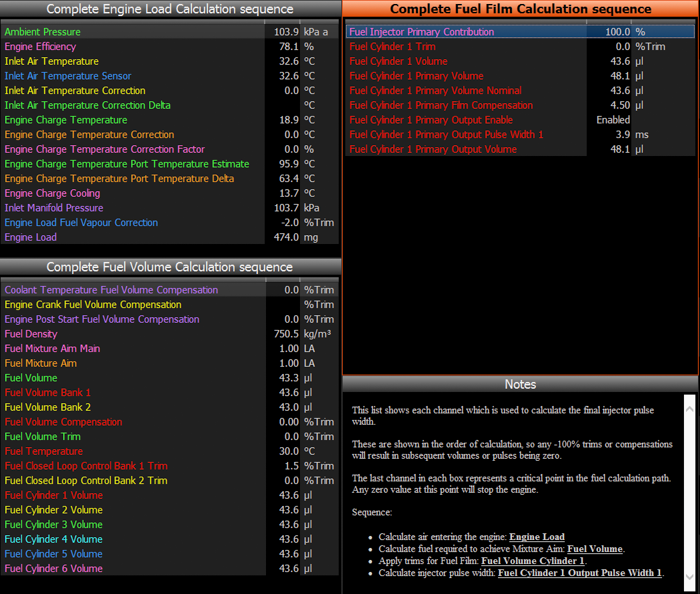
Here is what the M150’s diagnostic worksheet shows for the fuel calculation:

On the 330 we have, it has a Technique Tuning Stage 1 Turbo kit. The inlet manifold piping from behind the Mass Air Flow meter to the intake manifold is a metal pipe. This is easy to manufacture, and in the stock scenario is fine, as the MAF meter itself has a built-in air temperature sensor, which is in a plastic housing. As a result, it is fairly insulated from the engine bay heat. The problem here is that calibration data for this sensor is not readily available. Other sensors were, but as we don’t have the MS45.1 data, only MS45.0, it seems that the temperature sensor is different in US cars vs non-US. Thus, we have to build a calibration.

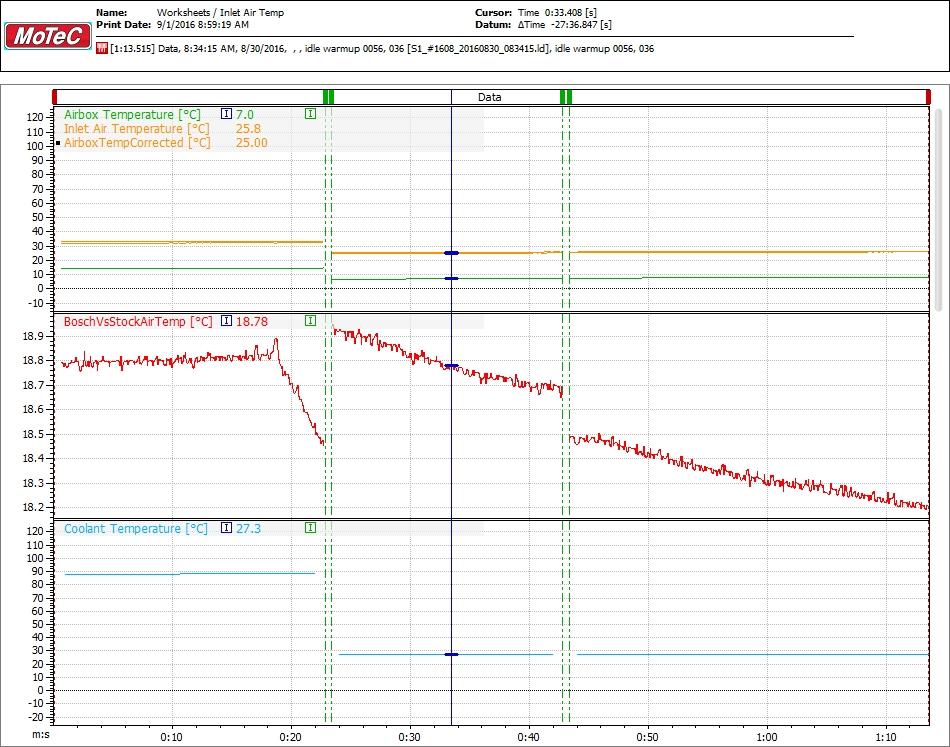
A Bosch air temperature with a known calibration curve was installed into the metal pipe mentioned earlier. Upon startup, if you compare the known sensor with the unknown, you can correct the sample at that voltage point for the unknown.

Over time you can correct the existing calibration curve. You would then put that data into a spreadsheet, and generate a fifth-order polynomial equation. This will create a smooth curve instead of the intermediate, messy curve that will be there during this comparison phase.

There are also ways to bench calibrate this, but in-situ is better, even if it takes longer.

A very nice feautre of the M150 is that you can use “Inlet Manifold Temperature” sensor to correct the Inlet Air Temperature reading, which is what is actually used in the Engine Load calculation. However, in this car we don’t have one of those. So we will make do with what we have.

Update

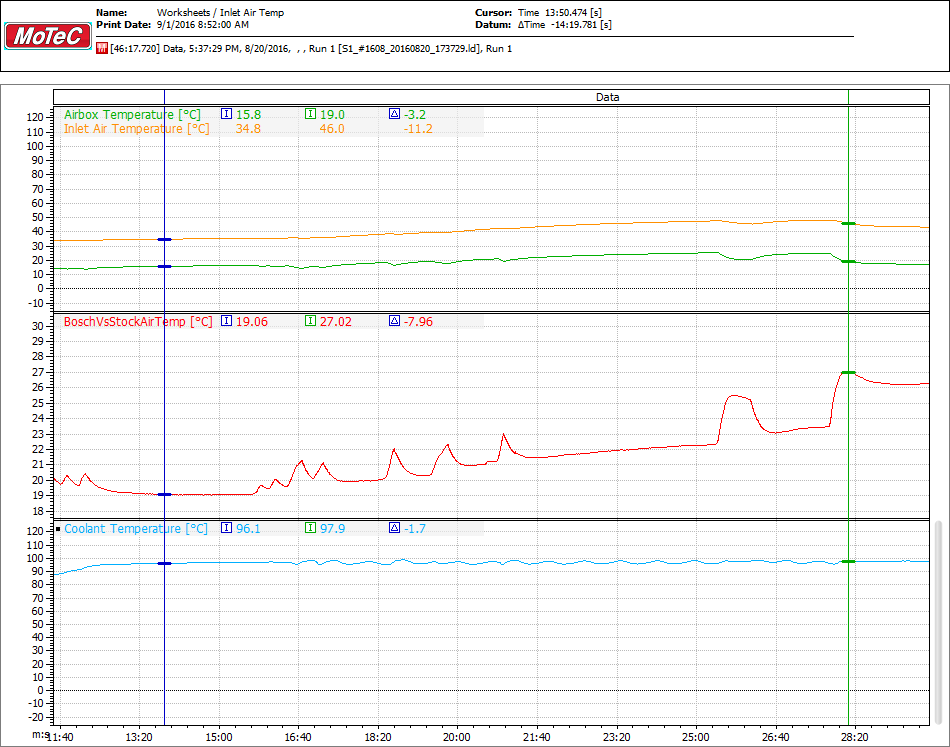
After further analysis, some trending shows an approximate 18 degrees Celcius deviation in the curve of the Bosch and stock sensor, and I added that to the existing calibration curve. After doing so it is pretty close so far.

As you can see, the deviation becomes much more than 18 degrees at points, and I’m fairly certain this is from heat soak, not actual temperature deviations.